Regla: Sú tala u sem hefur minnsta fjarlægð frá talnasafni M er miðgildi M.

Sönnun: Talnasafnið M hefur n stök. Við skilgreinum fjölskyldu af föllum, n að tölu, þannig að

Þessi falla-fjölskylda er sýnd hér á línuritinu:

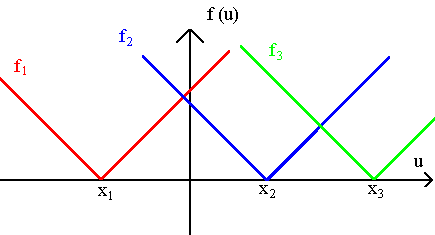
Þau eru greinilega allsstaðar samfelld í og diffranleg allsstaðar nema í einum punkti, u = x_k. Ennfremur er greinilegt að um hvert fall gildir að

Af framangreindu er ljóst að fallið f(u) = D(M,u) er líka samfellt í og ennfremur diffranlegt á bilunum milli gildanna í talnasafninu. Ferill f(u) er raunar bein strik milli allra punkta (x, f(x)) í M, og halli hans fæst af

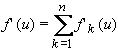
Með orðum sagt er f '(u) þannig jafnt fjölda talnanna í M vinstra megin við u á talnalínunni, að frádregnum fjölda talnanna í M hægra megin við u. Þess vegna er f '(u) negatíft (og f(u) minnkandi) meðan fleiri tölur eru hægra megin við u en vinstra megin. Af sömu ástæðu er f '(u) pósitíft (og f(u) vaxandi) þegar fleiri tölur eru vinstra megin en hægra megin. Þegar n er oddatala er frávikið minnst fyrir það gildi á u sem er í miðju talnasafnsins, en sé n jöfn tala liggur minnsta frávikið (f '(u) = 0) á bili milli miðjugildanna tveggja í talnasafninu.